This tab shows the calculations related to Energy Conservation. The law of conservation of energy states that the total energy of an isolated system remains constant; it is said to be conserved over time. This is the case in a 2D Truss system. This is an important concept from the science of kinetics which simply states that the work done on a body is equal to the energy expended on it.
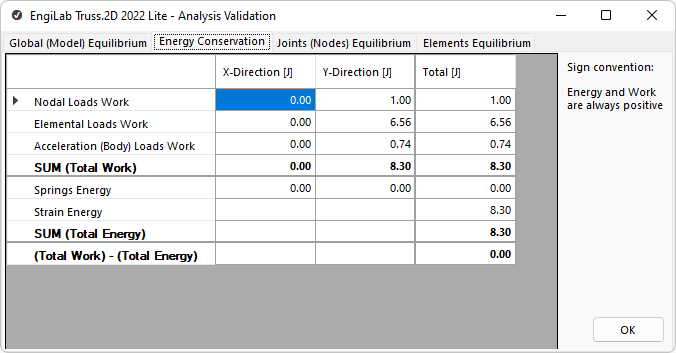
The program calculates the work of all external forces, in both X- and Y- directions:
•Work of Nodal Loads
•Work of Elemental Loads
•Work of Acceleration (Body) Loads
Elemental Loads and Acceleration (Body) Loads are handled as equivalent Nodal Loads for the Truss structure, as already mentioned in section What is a 2D Truss?
The program also calculates the Energy stored in the system, i.e. the following quantities:
•Springs Energy. It is the energy stored in springs due to Model deformation
•Strain Energy of all members. It is the energy stored in every Truss member due to its axial deformation.
If the analysis is successful and the model is in equilibrium, the work offered to the System by the external forces needs to be exactly the same as the Energy stored in the System as Spring Energy and Elastic Strain Energy. The program calculates the Total Work and the Total stored Energy and subtracts them. The result has to be zero or else there is a problem with the Model.
The formulas used for the calculation of the internal energy stored in the System are the following:
Spring Energy =1/2*K*x2,
where K is the stiffness of the spring (spring constant) and x is its extension or compression, i.e. the displacement of the corresponding DOF
Strain Energy =1/2*(E*A/L)*ΔL2 = F2*L/(2*E*A),
where E is the Elasticity Modulus of the Material, A is the Section Area, L is the original Length of the Element (i.e. in the undeformed state), ΔL is the Elongation of the Element, and F is its Axial Force.
The work of Nodal Loads (and the one of the equivalent Nodal Loads due to Elemental Loads and Body Loads) is calculated with the formula:
Work of Nodal Loads = 1/2*F*u,
where F is the Nodal Load and u is the displacement of the corresponding DOF from the Analysis. The reason why the factor 1/2 is used here is that the static force is applied slowly, increasing gradually from the value of zero to the F value (just like in a spring). So the work made by the external Force is not F*u, but rather 1/2*F*u.