The Consistent System of Units is the one shown in the form below. In fact, in this system, no specific units are used for any of the quantities, this is why all unit fields are empty. The Units can be anything (any compatible unit for the quantity in question), provided that some rules are followed, as explained next.
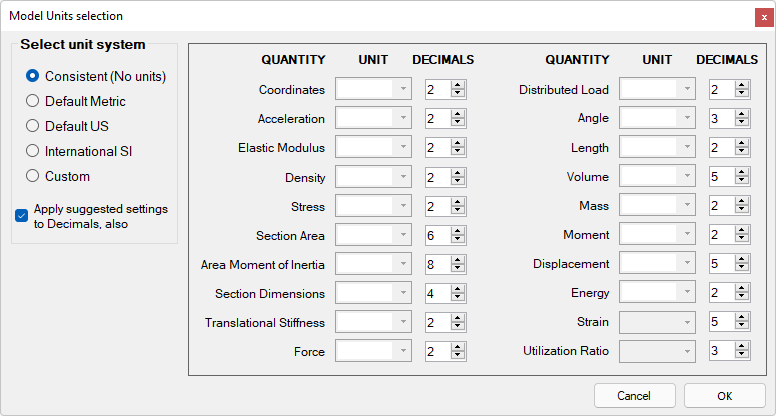
Consistent System of Units
How does a Consistent System of Units work?
Imagine Newton's Second Law of Motion. The equation is F = m * a,
where F is the force, m is the mass of the object and a is the acceleration. The second law states that the rate of change of momentum of a body over time is directly proportional to the force applied, and occurs in the same direction as the applied force. This law is global and it applies everywhere, no matter what units we use for the three quantities (Force, Mass and Acceleration). But these units need to be consistent, i.e. the units we use for mass and acceleration will define the unit we take for force when we apply the formula (without any conversions). For example if we use m=20 kg and a=10 m/s2, then we take F=200 and the unit of Force is then kg*m/s2, which means N (Newton). The result is therefore F=200 N. In a similar way, we can use the same formula with different units, as long as we always keep things consistent.
As long as we use Consistent Units, there is no need for any unnecessary conversions. What you give (inputs) will define what you take (outputs). When using Consistent Units, the program will not show any units, but the user needs to know what units he/she uses for the inputs. The outputs will simply comply. Below you can find a thorough explanation of how exactly this works and also instructions on using the most common units this way.
Implementation
All input data must be specified in consistent units. As a result, the analysis results will also comply to that system. The important point about using Consistent Units is the necessity to stick with units that work correctly together - not to mix units that do not have a correct relationship with each other.
In order to define a consistent system of units, you have to define first the primary (basic) units and then the derived units which are dependent on the primary units. We propose two different approaches for defining a consistent system of units, as described in detail below:
A. Consistent system of units based on Force
Define the three primary (basic) units for Force (F), Length (L), Time (T). For example you can choose to use kN, m, s (sec). The derived units are then the following:
Derived Unit |
Formula |
Formula explanation |
In our example (kN, m, s) |
|---|---|---|---|
Acceleration |
L/T2 |
(1 Length unit) / (1 time unit)2 |
m/s2 |
Mass * |
F·T2/L |
(1 force unit) / (1 acceleration unit) |
kN/(m/s2) = Mg = t * |
Density |
F·T2/L4 |
(1 mass unit) / (1 length unit)3 |
t/m3 |
Stress |
F/L2 |
(1 force unit) / (1 length unit)2 |
kN/m2 |
* The mass unit (in our example 1 t) is the mass that accelerates by the acceleration unit rate (in our example 1 m/s2) when the unit force (in our example 1 kN) is exerted on it.
B. Consistent system of units based on Mass
Define the three primary (basic) units for Mass (M), Length (L), Time (T). For example you can choose to use kg, m, s (sec). The derived units are then the following:
Derived Unit |
Formula |
Formula explanation |
In our example (kg, m, s) |
|---|---|---|---|
Acceleration |
L/T2 |
(1 Length unit) / (1 time unit)2 |
m/s2 |
Force * |
M·L/T2 |
(1 mass unit) · (1 acceleration unit) |
kg·m/s2 = N * |
Density |
M/L3 |
(1 mass unit) / (1 length unit)3 |
kg/m3 |
Stress |
M/L/T2 |
(1 force unit) / (1 length unit)2 |
N/m2 |
* The force unit (in our example 1 N) is the force required to accelerate the unit mass (in our example 1 kg) at the acceleration unit rate (in our example 1 m/s2).
Common consistent systems of units
Some common systems of consistent units are shown in the table below. Any column can be used for the inputs (and outputs) of the program.
Quantity |
SI (MKS) |
MTS |
mmNS |
US Unit (ft) |
US Unit (in) |
|---|---|---|---|---|---|
Length |
m |
m |
mm |
ft |
in |
Force |
N |
kN |
N |
lbf |
lbf |
Mass |
kg = N·s2/m |
t (tonne) = kN·s2/m |
t = N·s2/mm |
slug = lbf·s2/ft |
blob = lbf·s2/in |
Time |
s |
s |
s |
s |
s |
Stress |
Pa (N/m2) |
kPa (kN/m2) |
MPa (N/mm2 = MN/m2) |
lbf/ft2 |
psi (lbf/in2) |
Density |
kg/m3 |
t/m3 |
t/mm3 |
slug/ft3 |
lbf·s2/in4 |
Acceleration |
m/s2 |
m/s2 |
mm/s2 |
ft/s2 |
in/s2 |
As points of reference, the mass density of steel, the Young's Modulus of steel and the standard earth gravitational acceleration are given for each system in the table below.
Quantity |
SI (MKS) |
MTS |
mmNS |
US Unit (ft) |
US Unit (in) |
|---|---|---|---|---|---|
Steel density |
7850 kg/m3 |
7.85 t/m3 |
7.85×10-9 t/mm3 |
15.23151461 slug/ft3 (lbf·s2/ft4) |
7.34544493×10-4 blob/in3 (lbf·s2/in4) |
Steel Modulus of Elasticity (E) |
210×109 N/m2 |
210×106 kN/m2 |
210×103 MPa |
4,385,941,188.96153 lbf/ft2 (psf) |
30,457,924.9233 lbf/ft2 (psi) |
Earth Gravity acceleration |
9.80665 m/s2 |
9.80665 m/s2 |
9806.65 mm/s2 |
32.17404856 ft/s2 |
386.088583 in/s2 |
Notes:
•1 t (tonne) = 103 kg = 1 Mg. It is a mass that accelerates by 1 m/s2 when a force of 1 kN is exerted on it.
•1 slug = 1 lbf·s2/ft. It is a mass that accelerates by 1 ft/s2 when a force of 1 pound-force (lbf) is exerted on it.
•1 blob = 1 lbf·s2/in. It is a mass that accelerates by 1 in/s2 when a force of 1 pound-force (lbf) is exerted on it.
•1 MPa = 1 MN/m2 = 1 N/mm2
Practical example
The user chooses to use the MTS system, a common choice for structural engineering applications:
•Length: m
•Force: kN
•Time: s
EngiLab Truss.2D data have to be given as shown below:
Quantity |
Unit used |
Node Coordinates X, Y |
m |
Material Elastic Modulus E |
kPa = kN/m2 |
Material Density d |
t/m3 |
Section Area Α |
m2 |
Section Moment of Inertia I |
m4 |
Nodal Force F |
kN |
Elemental load f |
kN/m |
Spring Elastic Stiffness KX, KY |
kN/m |
Acceleration |
m/s2 |
The results will also comply to that system, thus they will be given as:
Quantity |
Unit used |
Node X, Y Displacement |
m |
Axial Force |
kN |
Axial Stress |
kPa |
Support reaction FX, FY |
kN |
Strain Energy |
kN·m=kJ |
Mass |
t=Mg |
Volume |
m3 |
* Rotations (where applicable) are ALWAYS given in RADIANS in a Consistent System of Units.
Note: In the above example, if one wants to apply self-weight to the structure, he/she can add the standard earth gravitational acceleration at the -Y direction as: aY = -9.80665 (i.e. m/s2)