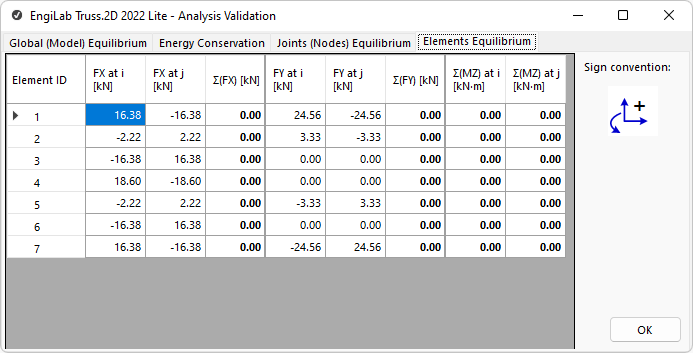
This tab shows the calculations related to the Equilibrium of Elements. After the Analysis, every Element of the 2D Truss needs to be in equilibrium state, i.e. the Sum of X-Forces and the Sum of Y-Forces need to be all zero for every Element. In addition, the Sum of moments of all Forces acting on the Element needs to be zero, at any point on the 2D plane.
Of course, any 2D Truss member which has only Axial Forces (no shear, no bending) and the Axial Force at Start i is the same as the Axial Force at End j (with opposite directions), satisfies these conditions, as a two-force body. See the illustration below where the Axial Forces Fi at i and Fj at j are decomposed into their two FX and FY components.
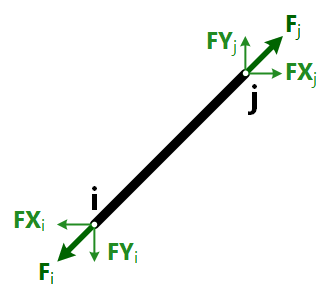
The program calculates these two components, the FX and FY Forces (in Global Axes) at both ends of each element, and the relevant Moments of these forces at i and j, as shown below.
In a 2D Truss, Elements do not have any loads (uniform or anything else) really applied on them. All loads are applied on the Nodes of the structure. In EngiLab Truss.2D, the user can apply self-weight of the members or other distributed loads (such as wind, snow and inertial forces), but the program automatically converts these loads to equivalent Nodal Loads. In the end, for the Analysis needs, there will be only Nodal Loads on the structure. Doing this, any effects of bending or shear on the Elements are neglected. The approach is explained below.
Assuming that a 2D Truss member carries a uniform load w (for example, in kN/m units), the total load is F=w*L (in kN), where L (in m, in this example) is the Length of the Element. For the Analysis, each Node (start and end Node) of this members takes a Force equal to F/2=w*L/2. This is shown schematically in the figure.