
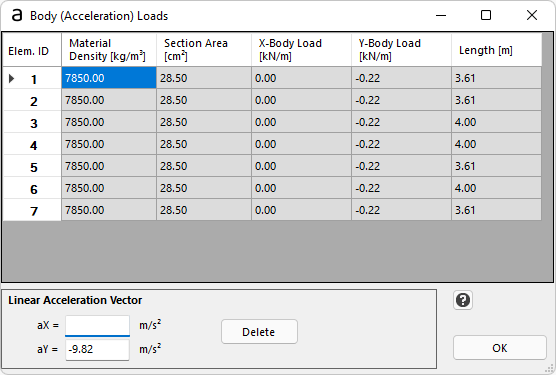
You can specify the X and Y components of an Acceleration vector acting on the Model. If the Model has Mass (Non-zero Density is defined for the Model's Material), then the acceleration will cause inertial body (Elemental) forces on the Elements of the Model, according to Newton's Second Law of Motion. These elemental forces are calculated automatically by the program and the results are shown on the form.
To apply an acceleration vector, type the values for the aX and aY acceleration components and press the ENTER on the keyboard. The model is updated automatically. The values of the X- and Y- Body Loads can be seen on the form (as read-only properties), together with the Material Density, the Section Area and the Length of each member.
The calculation is the following:
The total force on an element due to the Acceleration is: F=m*a (Newton's Second Law of Motion) = d*V * a = d*A*L * a,
where m is the mass, a is the acceleration, d is the density, V is the volume and L is the length of the Element.
Accordingly, the uniform Load (per unit length of the Element) is: f=F/L = d*A * a.
As a result, the uniform load applied on the Element due to an acceleration vector (in X or Y direction) is finally f=d*A*a
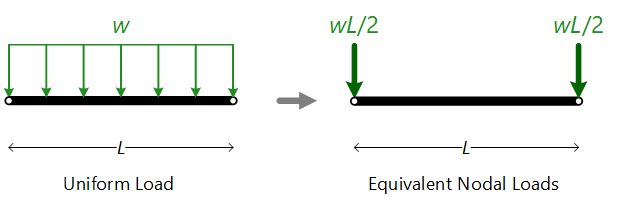
Important: In EngiLab Truss.2D all distributed loads are converted to equivalent Nodal Loads. In the end, for the Analysis needs, there will be only Nodal Loads on the structure. Doing this, the effects of bending on the Elements are neglected. The approach is shown schematically below.
Useful applications of body (Acceleration) loads
1. Define the self-weight of the Model or the self-weight of specific Elements
If you want to take into account the self-weight of Elements as an additional Elemental Load for each Element, then you have to provide the Material Density for the Material of each Element (See Materials) and also to define a Linear Acceleration Vector equal to the standard earth gravitational acceleration. A common practice is to put the earth gravitational acceleration with a minus (-) sign at the Y direction - this means gravity acting towards -Y global axis.
Example using Consistent Units: If the Consistent System of Units is used and you assume that you are using kN for forces, m for length and s for time, then the Material Density has to be given in t/m3 and you have to input -9.80665 (or simply -9.81) at the aY component of the Linear Acceleration Vector. This way, the self-weight will be applied to all Elements of the Model that have Mass (i.e. are assigned a Material which has a Density value). Note that Density is an optional property of a Material. If there is no Density for the Material of an Element, then the self-weight of the Element will be considered as zero and there will be no body load.
Using another System of Units: If Metric, US or another specific System of Units is used, then the Acceleration can be given using any Acceleration unit, as defined in the Predefined Systems section.
2. Define forces acting on a moving (accelerating) object
Acceleration is not only Gravity. If an object accelerates, then inertial forces are applied on it, provided that the object has Mass. For example, you can analyze a structure that is fixed on a moving (accelerating) vehicle. Even if there are no other loads, the acceleration of the vehicle will cause inertial forces on the object. By providing the X and Y components of the acceleration vector, you can calculate these forces and analyze the Model.